Introduction to Machine Learning and Data Mining

Ho, T.K., 1995, August. Random decision forests. In Document Analysis and Recognition, 1995., Proc of the Third Intl Conf on (Vol. 1, pp. 278-282). IEEE.

Kyle I S Harrington / kyle@eecs.tufts.edu

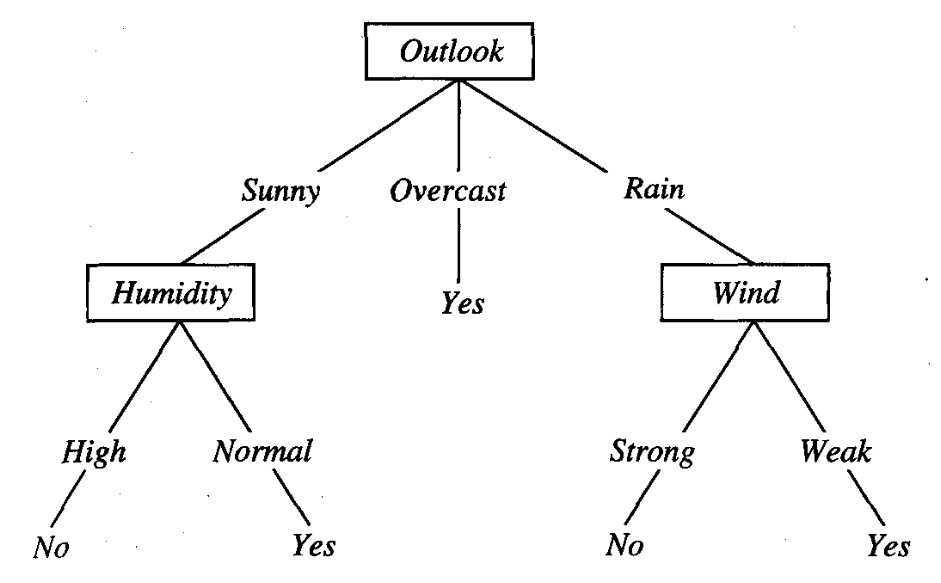
## Decision Trees ![Tennis Decision Tree](http://kephale.github.io/TuftsCOMP135_Spring2016/Lecture03/images/Mitchell_playTennis_decision_tree.png)

## Decision Trees What were the issues?

## Decision Trees What were the issues? - overfitting - weak generalizability

## Random decision forests Idea: Multiple trees can compensate for the bias of a single classifier How do we make *different* trees?

## Random decision forests Create decision trees that generalize by disregarding some features during classification 1. Choose a random subset of features 2. Train a decision tree on the subset

## Making a Decision with a Forest Use a forest of $t$ trees to classify $x$ as some class $c \in [1,n]$ The prediction of a tree $T_i$ for instance $x$ is $P(c|T_i(x))$, representing the probability of class $c$ at a leaf of $T_i$, when fully split $P(c|T_i(x))=1$. The discriminant function is $g_c(x) = \frac{1}{t} \displaystyle \sum^t_j P(c|T_j(x))$ and the classification is the $c$ that maximizes $g_c(x)$.

## Experiments - Dataset: handwritten digits (MNIST) - Features: 20x20 Pixels (400 features) - Compare 2 branching methods - Test an additional set of features that include conjunctions/disjunctions of neighboring pixels (852 features)

## Central axis projection branching - Calculate the mean of each class - Define a central axis between the means of the two most distant classes - Project all points onto central axis - Search with incremental steps along axis for threshold that optimizes accuracy Very fast, but produces large trees

## Perceptron branching - Calculate the mean of each class - Find the two most distant classes - Label all instances based on the nearest of these 2 class centroids - Use perceptron learning to learn the line that separates both classes Slow, but produces compact trees

## Experiments ![Ho 1995 Table 1](images/Ho_1995_Table1.png)

## Experiments ![Ho 1995 Figure 1](images/Ho_1995_Figure1.png) Random forest of 20 trees with 100 or 200 dimensional feature subspaces created with central axis projection branching.

## Experiments ![Ho 1995 Figure 2](images/Ho_1995_Figure2.png) Random forest of 10 trees with 100 or 200 dimensional feature subspaces created with perceptron branching.

## What Next? Assignment 5 due 04/26 Project Presentations