Introduction to Machine Learning and Data Mining

Kyle I S Harrington / kyle@eecs.tufts.edu

Some slides adapted from Geoff Hinton and David Touretzky

## Neural Networks - perceptron - multi-layer networks - backpropagation - deep neural networks - recurrent networks - evolutionary neural networks

Linear Regression

Linear weighting of N-dimensional instances

$y = \vec{w} \cdot \vec{x} + b$

where $| \vec{x} | = N$, $b$ is the intecept, and $\vec{w}$ are real-valued weights.

Linearity Doesn't Add Up

Multiple layers of linear units do not improve performance

$\vec{y} = V * ( U * \vec{x} ) = ( V * U ) * \vec{x}$

The weights from both layers, U and V, are equivalent to a single layer, $W = V * U$

We suspect we need multiple layers to support higher-order interactions between inputs, what type of units would be better?

## Perceptron ![McCullough-Pitts Neuron](images/Mcculloch_pitts.svg) $x_i$ input value $i$, $w$ weight, $\sigma$ activation function, $y$ output

Activation Function

Activation function is applied sum of weighted inputs: $\sigma( \displaystyle \sum_i w_i x_i ) = y$

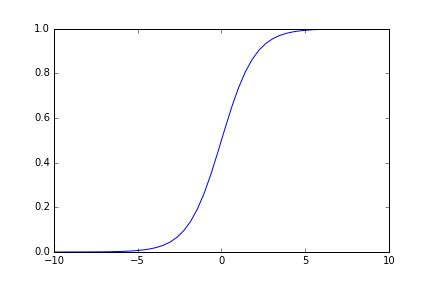
Logistic: $f(x) = \frac{1}{1+e^-x}, f(x)' = f(x) (1 - f(x))$

Alternatively hyperbolic tangent: $f(x) = tanh(x), f(x)' = \frac{1}{cosh(x)^2}$

## Neural Networks A neural network is a collection of artificial neurons interconnected with directional edges denoting the flow of information from input to output and potentially over time. Features: - representing higher-order interactions and dependencies - tolerant to noise - slow to train - fast to evaluate

## Network Topology The *topology* of a neural network describes the connectivity of neurons in the network - **1-layer**: linear model - **2-layers**: universal approximation - **deep**: higher-order concepts - **recurrent**: memory

## Single Layer Networks ![Single layer network](images/single_layer_classification.png)

## 2 Layer Networks ![2-layer Feedforward network](images/two_layer_classification.png)

## 3 Layer Networks ![3-layer Feedforward network](images/three_layer_classification.png)

## Example Networks ![A Neural Network for Setting Target Corn Yields](http://abe-research.illinois.edu/remote-sensing/Papers/ANN_files/image4.gif) A Neural Network for Setting Target Corn Yields (Liu, Goering, Tian, 2001)

## Training Neural Networks - backpropagation (for feedforward NNs) - backpropagation through time (for recurrent NNs) - evolutionary optimization (for discovering topology and parameters)

## Backpropagation [Hinton's Backpropagation Slides (Lecture 3d)](http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec3.pdf)

## Deep Networks ![Deep Feedforward Network](images/deep_network.png) Image from [RSIP vision](http://www.rsipvision.com/exploring-deep-learning/)

Deep Networks

Convolutional neural networks perform better at image labeling tasks (object detection) with greater depth.

Urban, G., Geras, K.J., Kahou, S.E., Aslan, O., Wang, S., Caruana, R., Mohamed, A., Philipose, M. and Richardson, M., 2016. Do Deep Convolutional Nets Really Need to be Deep (Or Even Convolutional)?. arXiv preprint arXiv:1603.05691.

## Recurrent Networks ![Recurrent Network](images/recurrent_network.png)

## Backpropagation Through Time ![Unfolding recurrent network](https://upload.wikimedia.org/wikipedia/en/e/ee/Unfold_through_time.png)

## Evolutionary Optimization - GNARL, evolution of neural network topology - NEAT, recombination of neural network topology - HyperNEAT, evolution of hyper-NNs for generative weight encoding

## Evolutionary Algorithm - Use a population of N models Iterate until convergence: 1. Test/evaluate all models 2. Select better models (i.e. fitness proportionate selection) 3. Vary/adapt selected models (i.e. adjust weights, add/remove neurons)

GNARL

Left, network on generation 1, and right, network on generation 765, for an example finite-state problem.

Angeline, P.J., Saunders, G.M. and Pollack, J.B., 1994. An evolutionary algorithm that constructs recurrent neural networks. Neural Networks, IEEE Transactions on, 5(1), pp.54-65.

NeuroEvolution of Augmenting Topologies

Tracks novel model changes (i.e. when a neuron is added)
Solves the problem of recombining NNs (align NNs and splice)
Tracks species of neural networks (groups similar NNs)

Stanley, K.O. and Miikkulainen, R., 2002. Evolving neural networks through augmenting topologies. Evolutionary computation, 10(2), pp.99-127.

Hyper-Neural Networks

Problem: Make a 4-legged robot walk as far/fast as possible

The robot.

The control NN.

Clune, J., Stanley, K.O., Pennock, R.T. and Ofria, C., 2011. On the performance of indirect encoding across the continuum of regularity. Evolutionary Computation, IEEE Trans. on, 15(3), pp.346-367.

Hyper-Neural Networks

A hyper-neural network (HNN) takes coordinates for each weight in a network and returns the weight's value.

$HNN(N_{i},N_{o}) = w_{i,o}$, where $N_i$ and $N_o$ are in/out neurons

Stanley, K.O., D'Ambrosio, D.B. and Gauci, J., 2009. A hypercube-based encoding for evolving large-scale neural networks. Artificial life, 15(2), pp.185-212.

Hyper-Neural Networks

Left, weights are generated by a hyper-NN, and right, weights are optimized directly.

Clune, J., Stanley, K.O., Pennock, R.T. and Ofria, C., 2011. On the performance of indirect encoding across the continuum of regularity. Evolutionary Computation, IEEE Trans. on, 15(3), pp.346-367.

## Projects - Update - Due 04/12 - Submit 5 slides - Including: title, 2 1-slide summaries of previous papers, current progress - Presentations - Paper

## Presentations - 3.5 days - 6 minutes per person - 3 days that start with 15-min discussion of a recent paper

## What Next? Support vector machines